ICA算法之数学原理
ICA的数学推导
ICA算法的思路比较简单,但是推导过程比较复杂(可以参考matrix手册推导一下),本文只是梳理了推理路线,忽视了具体的推导过程,如果不详之处,还望见谅。
假设我们有n个混合信号源$X\subset{R^{n}}$和n个独立信号$S\subset{R^{n}}$,且每个混合信号可以由n个独立信号的线性组合产生,即:
\[X=\left[ \begin{matrix} x_1&\\ x_2&\\ ...&\\ x_n& \end{matrix} \right]\] \[S=\left[ \begin{matrix} s_1&\\ s_2&\\ ...&\\ s_n& \end{matrix} \right]\] \[X=AS => S=WX,W=A^{-1}\]假设我们现在对于每个混合信号,可以取得m个样本,则有如下$n*m$的样本矩阵:
\[D=\left[ \begin{matrix} d_{11}&d_{12}&...&d_{1m}&\\ ...&\\ d_{n1}&d_{n2}&...&d_{nm}\\ \end{matrix} \right]\]由于S中的n个独立信号是相互独立的,则它们的联合概率密度为:
\[p_S(s)=\Pi_{i=1}^{n}p_{s_i}(s_i)\]由于$s=Wx$,因此我们可以得出:
\[p_X(x)=F^{'}_{X}(x)=|\frac{\partial{s}}{\partial{x}}|*p_S(s(x))=|W|*\Pi_{i=1}^{n}p_{s_i}(w_ix)\]考虑目前有m个样本,则可以得到所有样本的似然函数:
\[L=\Pi_{i=1}^{m}(|W|*\Pi_{j=1}^{n}p_{s_j}(w_{j\cdot}d_{\cdot{i}}))\]取对数之后,得到:
\[lnL=\Sigma_{i=1}^{m}\Sigma_{j=1}^{n}lnp_{s_j}(w_{j\cdot}d_{\cdot{i}})+mln|W|\]之后只要通过梯度下降法对$lnL$求出最大值即可,即求使得该样本出现概率最大的参数$W$。
此时假设我们上面的各个独立信号的概率分布函数为sigmoid函数,但是不确定这里的g函数和下面fastICA中的g函数是否有关联):
最终,我们求得:
\[\frac{\partial{lnL}}{\partial{W}}=Z^TD+\frac{m}{|W|}(W^*)^T\]其中:
\[Z=g(K)=\left[ \begin{matrix} g(k_{11})&g(k_{12})&...&g(k_{1m})&\\ ...&\\ g(k_{n1})&g(k_{n2})&...&g(k_{nm})\\ \end{matrix} \right]\] \[g(x)=\frac{1-e^x}{1+e^x}\] \[K=WD\] \[D=\left[ \begin{matrix} d_{11}&d_{12}&...&d_{1m}&\\ ...&\\ d_{n1}&d_{n2}&...&d_{nm}\\ \end{matrix} \right]\]由于伴随矩阵具有以下性质:
\[WW^*=|W|I\]因此我们可以求出:
\[\frac{\partial{lnL}}{\partial{W}}=Z^TD+m(W^{-1})^T\]因此可以得到梯度下降更新公式:
\[W=W+\alpha(Z^TD+m(W^{-1})^T)\]至此,ICA的基本推理就此结束。下面我们来看一下fastICA的算法过程(没有数学推理)。
fastICA的算法步骤
观测信号构成一个混合矩阵,通过数学算法进行对混合矩阵A的逆进行近似求解分为三个步骤:
- 去均值。去均值也就是中心化,实质是使信号X均值是零。
- 白化。白化就是去相关性。
- 构建正交系统。
在常用的ICA算法基础上已经有了一些改进,形成了fastICA算法。fastICA实际上是一种寻找$w^Tz(Y=w^Tz)$的非高斯最大的不动点迭代方案。具体步骤如下:
- 观测数据的中心化(去均值)
- 数据白化(去相关),得到z
- 选择需要顾及的独立源的个数n
- 随机选择初始权重W(非奇异矩阵)
- 选择非线性函数g
- 迭代更新:
- $w_i \leftarrow E\{zg(w_i^Tz)\}-E\{g^{'}(w_i^Tz)\}w$
- $W \leftarrow (WW^T)^{-1/2}W$
- 判断收敛,是下一步,否则返回步骤6
- 返回近似混合矩阵的逆矩阵
fastICA中常用的g函数
参考《Indepdent Componet analysis》一书,找到了如下几点:
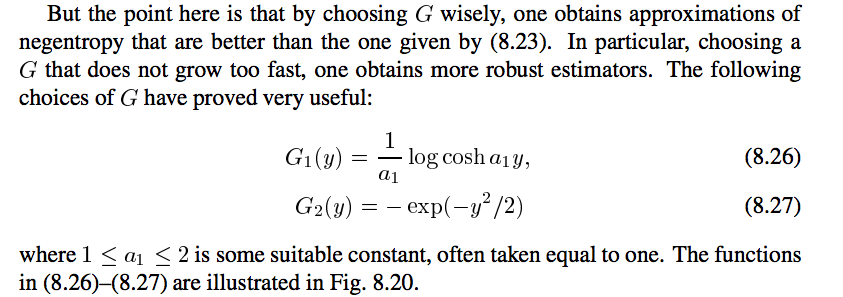
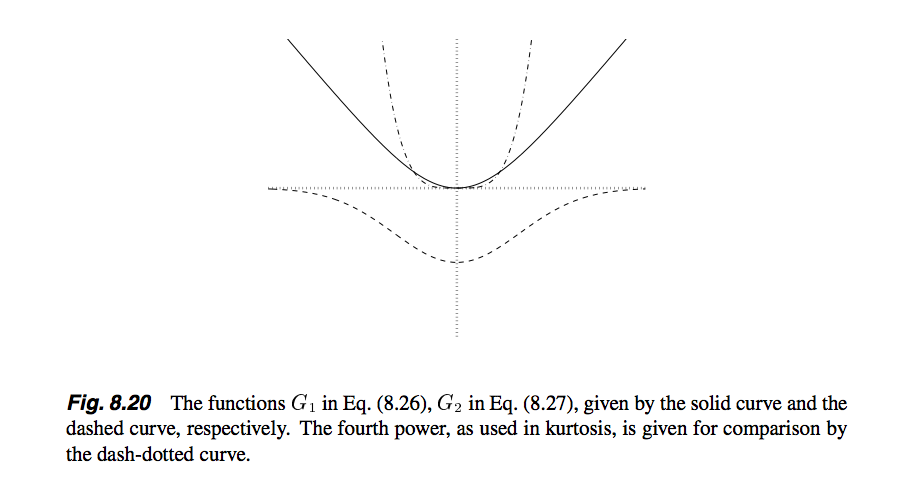

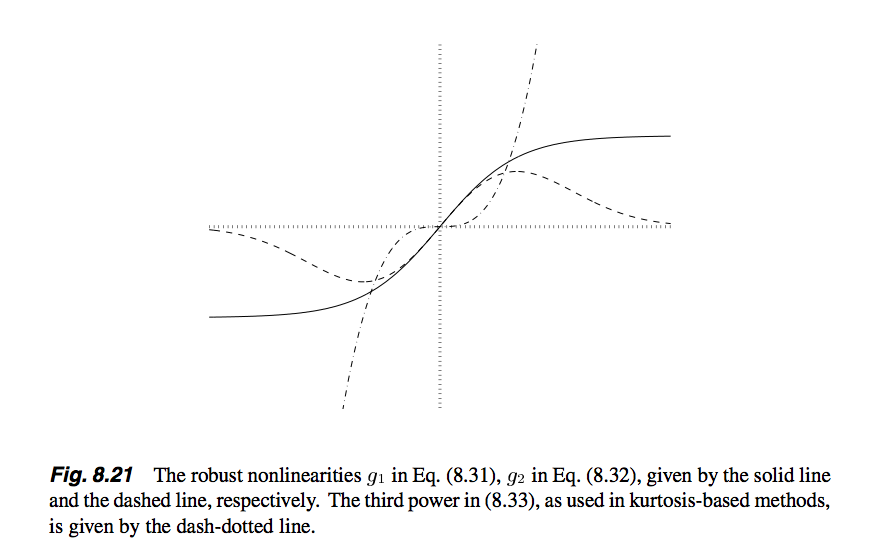
也就是说,G函数常用的有logcosh和和exp函数,它们对应的导数就是g函数,并且文中还提供了一种g函数,即cube函数。
具体细节读者可以参考“参考”里面的《Indepdent Componet analysis》一书,里面有详细的介绍。
白化的补充
白化其实就是将原始数据$X$,通过一个线性变换矩阵$V$,变成$Z$,即:
\[Z=VX\]且Z有如下性质:
\[Cov(ZZ^T)=I\]假设$X$的协方差矩阵为$C_x=E\{XX^T\}=PDP^T$,$P$是$C_x$的单位特征向量,$D$为特征值组成的对角阵,那么,可以知道当:
\[V=D^{-1/2}P^T\]的时候,$ZZ^T$的协方差矩阵为一个单位阵。
这里说明一下,PCA保证各个信号之间无相关性(即协方差矩阵的非对角元素为0),而白化则是保持无相关性的同时,保证对角元素值为1。白化并不是唯一的,只要保证最后产生的$Z$的协方差矩阵是单位阵即可。
参考
ICA(独立成分分析)在信号盲源分离中的应用
史上最直白的ICA教程
史上最直白的ICA教程pdf
Independent Component Analysis:
Algorithms and Applications
白化
Indepdent Componet analysis