DeepLearning

Group Normalization简介

Posted by SkyHigh on April 7, 2018

Group Normalization简介

之前我已经在normalization上单独做了一章，分别概述了Batch Norm、Layer Norm、Weight Norm以及selu在加速网络收敛上的效果。不过，最先提出这个思路的是BN，之后的则是在其基础上进行改进（或者照瓢画葫芦再来一套？），因此此处我们也是直接将GN的效果有BN直接进行比较（作者在论文也是这么做的）。虽然normalization在NLP任务上并不如CV里常用，但是这种学习的思想还是直接去了解的（万一哪天normalization在某类NLP任务上搞了个大新闻，还是很excited的）。
对上一节有兴趣的读者可以参考：加速网络收敛——BN、LN、WN与selu

Group Normalization的原理

在我看来，GN有三个点起码比BN“好用”：

  • BN需要区分train和evaluate过程，而GN不用
  • BN对batch size敏感，而GN与batch size独立（包括loss与accuracy等），BN的性能会随着训练的batch size变小而集聚下降（让BN在某些受内存限制而需要输入小batch的任务上效果不好）
  • 小batch size的时候，GN效果要比BN好（原因就是第二点）

而GN在速度上，通常比BN要慢，这是因为GN相对于BN来说，有额外的transpose与reshape操作，当层数加深的时候，训练速度也按比例下降。

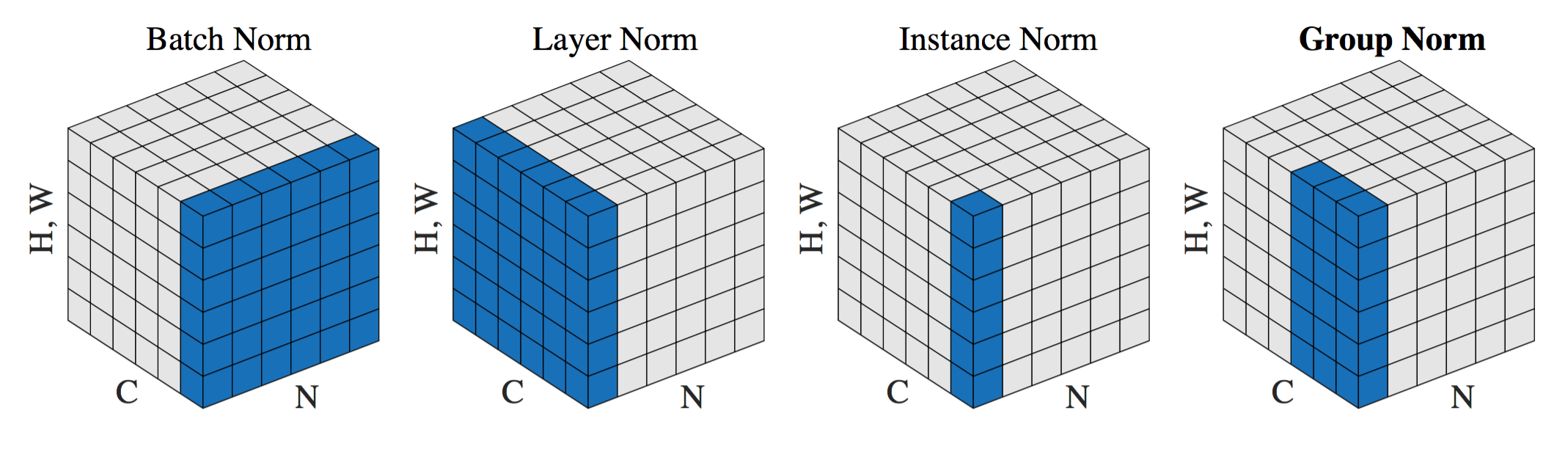
从上图可以看到，其实各个方式只是在不同维度、粒度上进行变化。假设输入的shape为(N, C, H*W)，则有：

  • Batch Norm：在N维度做normalization，计算N*H*W维度的均值与标准差
  • Layer Norm：在C维度做normalization，计算C*H*W维度的均值与标准差
  • Instance Norm：计算每一个H*W的均值与标准差
  • Group Norm：在G维度做normalization，计算(C//G)*H*W维度的均值与标准差

可以看到，其实GN是LN与IN的折中方法。

代码实现

import tensorflow as tf

def group_norm(x, G=32):
    """
        x: [B, H, W, C]
        G: group numbers
    """

    epsilon = 1e-8
    with tf.variable_scope('gn'):
        # [B, H, W, C] -> [B, C, H, W]
        B, H, W, C = x.get_shape().as_list()
        x = tf.transpose(x, (0, 3, 1, 2))
        x = tf.reshape(x, (B, G, C // G, H, W))
        mean, var = tf.nn.moments(x, (2, 3, 4), keep_dims=True)
        x = (x - mean) / tf.sqrt(var + epsilon)
        gamma = tf.get_variable('gamma', (C, ), initializer=tf.constant_initializer(1.))
        beta = tf.get_variable('beta', (C, ), initializer=tf.constant_initializer(0.))
        x = tf.reshape(x, (B, C, H, W))
        gamma = tf.reshape(gamma, (1, C, 1, 1))
        beta = tf.reshape(beta, (1, C, 1, 1))
        x = gamma * x + beta
        x = tf.transpose(x, (0, 2, 3, 1))
        return x

if __name__ == '__main__':
    with tf.Session() as sess:
        feature_map = tf.random_normal(shape=(32, 7, 7, 64))
        feature_map_after_gn = group_norm(feature_map)

        sess.run(tf.initialize_all_variables())

        feature_map_out, feature_map_after_gn_out = \
                                sess.run([feature_map, feature_map_after_gn])
        print(feature_map_out)
        print(feature_map_after_gn_out)

实验效果

笔者尝试跑了下Reference里第二个repo，各个任务上的实验效果可以直接参看repo。有兴趣的同学也可以尝试跑一下。构建方法比较简单（如上实现过程），就不重复造轮子了。

References