Capsule Networks
什么是capsule
CNN的问题
传统的CNN网络在提取特征的时候是先考虑局部特征再整合,并没有考虑整体特征的联动。CNN每一层的每个神经元输出是一个scalar,它表示对某个特征的似然(这个特征是否出现的概率),这对于模型来说,有时候会把问题考虑的太简单了。比如输入一张脸,那么网络在学习的时候,会单独对特征判断(比如有眼睛、有鼻子、有嘴巴),并且整合上述判断给出这个是否是人脸。如果上述特征都有,但是眼睛的大小、比例、方向都不是正常的人的样子,模型也会识别出来。也就是说,CNN网络单纯依靠来自局部的判断而“草率”的下决定,无视了特征之间的关系(空间位置关系、大小比例关系等)。并且,CNN需要考虑各种情况的样本(比如旋转各种角度的人脸)来应对测试集各种可能出现的情况。
如果需要学习应变不同方向、器官比例的脸,那么CNN需要加深网络深度。比如第一层先去识别脸上各个器官,第二层去识别各个器官的角度,第三层去识别器官的比例大小。如果一个任务很复杂,则需要堆叠更多的层数。
capsule的出现
那么,有没有办法解决这些问题呢?试想我们将每个神经元替换成一组神经元,那么此时这组神经元输出的就不是一个scalar而是一个vector。并且我们假设这个vector的模长表示原来的scalar的意义(特征似然性),而用方向表示这个特征的一些属性(与word embedding的idea相似),那么我们通过多组神经元就可以去学习到上面需要通过多层网络学习到的东西。那么这个一组神经元就被称为capsule(胶囊)。
动态路由(dynamic routing)
动态路由描述的是如何从前一层的多个capsules去计算出后一层的多个capsules。
transformation
考虑到前一层的每个capsule表示一个特征,这些特征在进入下一层前需要统一。比如前一层的两个特征:眼睛和嘴巴,它们的宽度不同,$width_{mouth}=30, width_{eye}=20$,但是它们可以按比例放缩出相同大小的对下一层的脸的特征描述,比如眼睛对应的参数$W_e=3$,嘴巴对应的参数$W_m=2$,那么脸的宽度为$width_{mouth} \times W_m==width_{eye} \times W_e==60$。因此,假设前面有$n$个capsules,每个capusle表示为$u_i, u_i \in R^{k}$,transformation matrix中每个元素为$W_{ij}, W_{ij} \in R^{k \times p}$,则转移后的prediction vector $\hat{u_{j \mid i}}$可以表示为:
\[\hat{u_{j \mid i}}=W_{ij} \times u_i\]vote
假设对每个output capsule,我们有$n$个(与前一层capsule个数对应)prediction vector,那么我们如何通过这$n$个vector构造output capsule呢?从聚类角度考虑,假设$p(i,j)=c_{ij}, \Sigma_{j}c_{ij}=1$表示输入i属于j的概率,那么我们可以让输出$s_j$表示如下:
\[s_j=\Sigma_i c_{ij}\hat{u_{j \mid i}}\]squash
获得每个输出capsule表示$s_j$后,我们还需要考虑将它进行放缩以便让每个向量的模长具有概率意义。
\[v_j=\frac{\parallel s_j \parallel^2}{1 + \parallel s_j \parallel^2}\frac{s_j}{\parallel s_j \parallel}\]iterative dynamic routing
在上述环节中,我们没有讲合理的$c_{ij}$如何得到。假设这是一个聚类问题,那么我们肯定希望$\hat{u_{j \mid i}}$与$v_j$越相似,那么$c_{ij}$值应该越大。假设一开始$c_{ij}$等概率,结合之前的步骤,我们可以有如下迭代过程:

paper中给出迭代次数为3次。训练和测试过程都需要做动态路由。
小小实验
现在我们尝试构建下图的capsule网络。
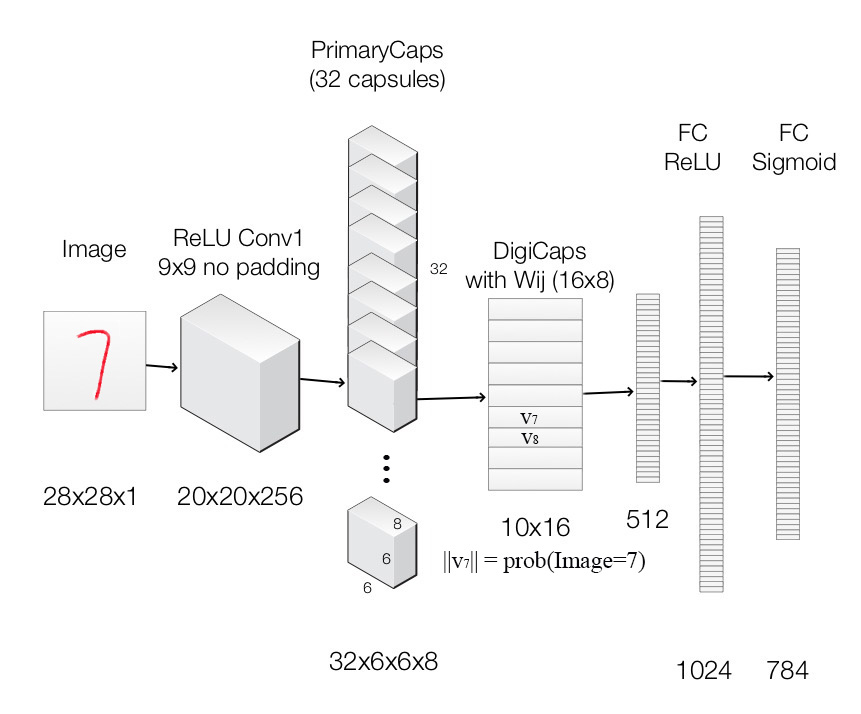
各层网络结构如下:
| Layer Name | Apply | Output shape |
|---|---|---|
| Image | Raw image array | 28x28x1 |
| ReLU Conv1 | Convolution layer with 9x9 kernels output 256 channels, stride 1, no padding with ReLU | 20x20x256 |
| PrimaryCapsules | Convolution capsule layer with 9x9 kernel output 32x6x6 8-D capsule, stride 2, no padding | 6x6x32x8 |
| DigiCaps | Capsule output computed from a Wij (16x8 matrix) between ui and vj (i from 1 to 32x6x6 and j from 1 to 10). | 10x16 |
| FC1 | Fully connected with ReLU | 512 |
| FC2 | Fully connected with ReLU | 1024 |
| Output image | Fully connected with sigmoid | 784 (28x28) |
现在我们主要来看看capsule之间是完成操作的。假设输入的是$(B, 1192, 8)$的capsule,B为batch size,那么:
transformation
# (batch_size, 1, input_num_capsule, input_dim_capsule)
expand_inputs = K.expand_dims(inputs, axis=1)
# (batch_size, num_capsule, input_num_capsule, input_dim_capsule)
expand_inputs = K.tile(expand_inputs, (1, self.num_capsule, 1, 1))
# (batch_size, num_capsule, input_num_capsule, dim_capsule)
u_hat = K.map_fn(lambda x: K.batch_dot(x, self.W, axes=[2, 3]), expand_inputs)
squash
def squash(s, axis=-1):
"""
Squash function. This could be viewed as one kind of activations.
"""
squared_s = K.sum(K.square(s), axis=axis, keepdims=True)
scale = squared_s / (1 + squared_s) / K.sqrt(squared_s + K.epsilon())
return scale * s
dynamic routing
# (batch_size, num_capsule, input_num_capsule)
b = K.zeros((K.shape(u_hat)[0], self.num_capsule, self.input_num_capsule))
for i in xrange(self.num_routing):
# (batch_size, num_capsule, input_num_capsule)
c = softmax(b, axis=1)
# (batch_size, num_capsule, dim_capsule)
s = K.batch_dot(c, u_hat, axes=[2, 2])
squashed_s = squash(s)
if i < self.num_routing - 1:
# (batch_size, num_capsule, input_num_capsule)
b += K.batch_dot(squashed_s, u_hat, axes=[2, 3])
return squashed_s
margin loss
这个loss是计算对10个数字每一类的分类误差的。如果后面加了重构部分(重构回28*28的图),可以用mse来计算重构误差。
def margin_loss(y, pred):
"""
For the first part of loss(classification loss)
"""
return K.mean(K.sum(y * K.square(K.maximum(0.9 - pred, 0)) + \
0.5 * K.square((1 - y) * K.maximum(pred - 0.1, 0)), axis=1))
完整代码
这个模型跑起来很慢(我的机器太差了,跑的太慢),建议在GPU上跑,或者在好的CPU服务器上跑。完整代码请参考:CapsNet。
References
- Dynamic Routing Between Capsules
- “Understanding Dynamic Routing between Capsules (Capsule Networks)”
- “Understanding Matrix capsules with EM Routing (Based on Hinton’s Capsule Networks)”
- Does the Brain do Inverse Graphics?
- Capsule Network Performance on Complex Data
- 胶囊网络结构Capsule初探
- Xiaofeng Guo’s Capsule Network repo
- Understanding Hinton’s Capsule Networks, Part I - IV