频繁项集和关联规则
很早之前接触过频繁项集和关联规则挖掘的两个算法Apriori和FP-Growth,但是一直没有在实际中应用过,因此当时学的内容基本都忘得差不多了。最近要交数据挖掘课的作业,因此趁此机会,算是复习一下。以后忘记了,也好翻出来看看,看书真的有点头疼……
1.概念
事务、支持度、频繁项集和k项集等概念
事务就是下图中的样子:
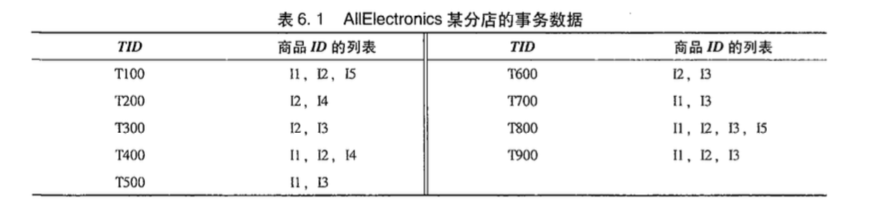
支持度,是指某个集合在所有事务中出现的频率,可以用$P(A)$表示。
频繁项集,是指支持度大于等于最小支持度(min_sup)的集合。
k项集,是指包含k个项(item)的集合。
闭频繁项集,设为频繁项集S,如果不存在真超集V,使得V的支持度等于S的支持度,则S为闭频繁项集。
极大频繁项集,设频繁项集S,如果其所有的真超集V均不频繁,则S为极大频繁项集。
置信度,是指某个关联规则的概率,可以用$P(B|A)$表示。
关联规则,表示的是在某个频繁项集的条件下推出另一个频繁项集的概率。如果该关联规则的置信度大于等于最小置信度,则为强关联规则。
2.频繁项集的挖掘算法
Apriori
从1-项集到n-项集,在每个k-项集中找出满足最小支持度的k-频繁项集,然后通过k-频繁项集组合,得到(k+1)-项集,之后再选出满足要求的(k+1)-频繁项集,以此类推,直到找到最大的k-项集为止。
下面通过一个比较好的例子来看,直接从书里摘出来:
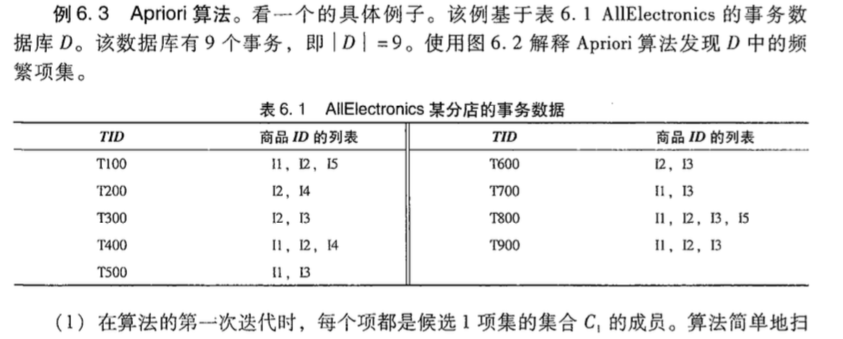
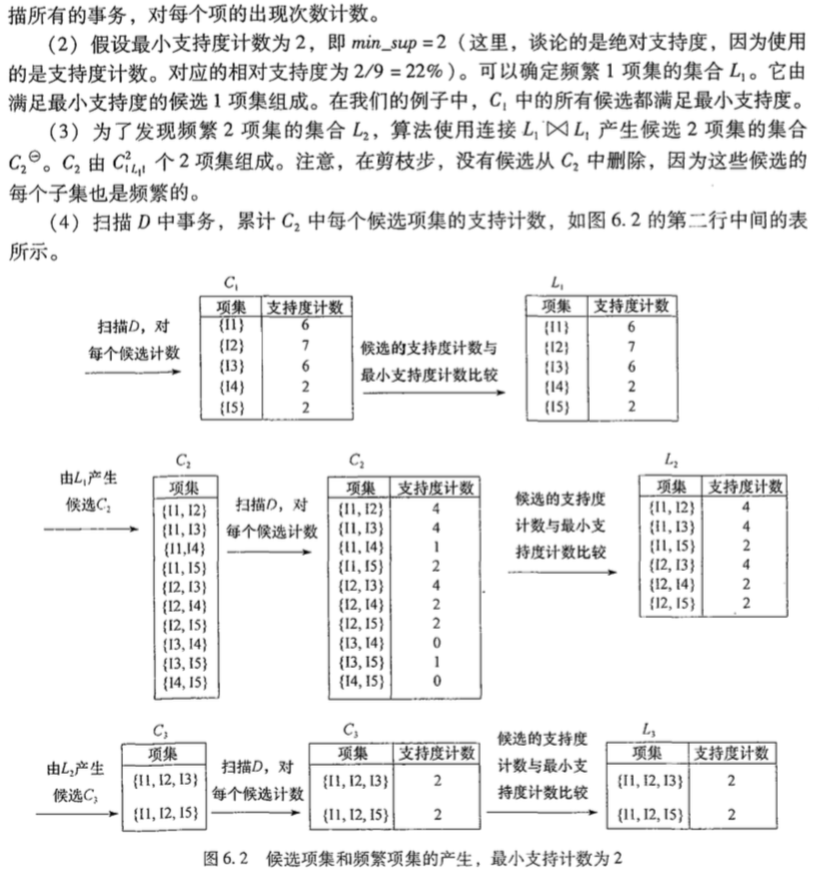


导出关联规则
这里我们只例举$X=\{I1,I2,I5\}$这个频繁项集。


FP-Growth
通过频繁项集增长模式来获取频繁项集,它的效率比Apriori高出很多。可以通过FP-Growth寻找频繁项集,之后使用上面的方法导出关联规则。
同样以上面的例子为例,直接截图:

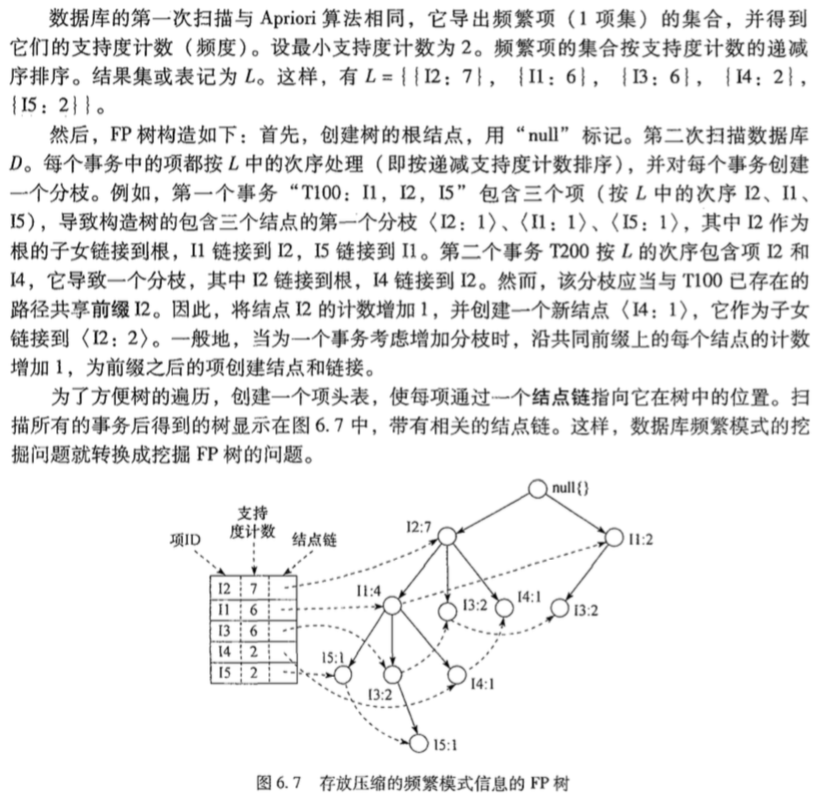


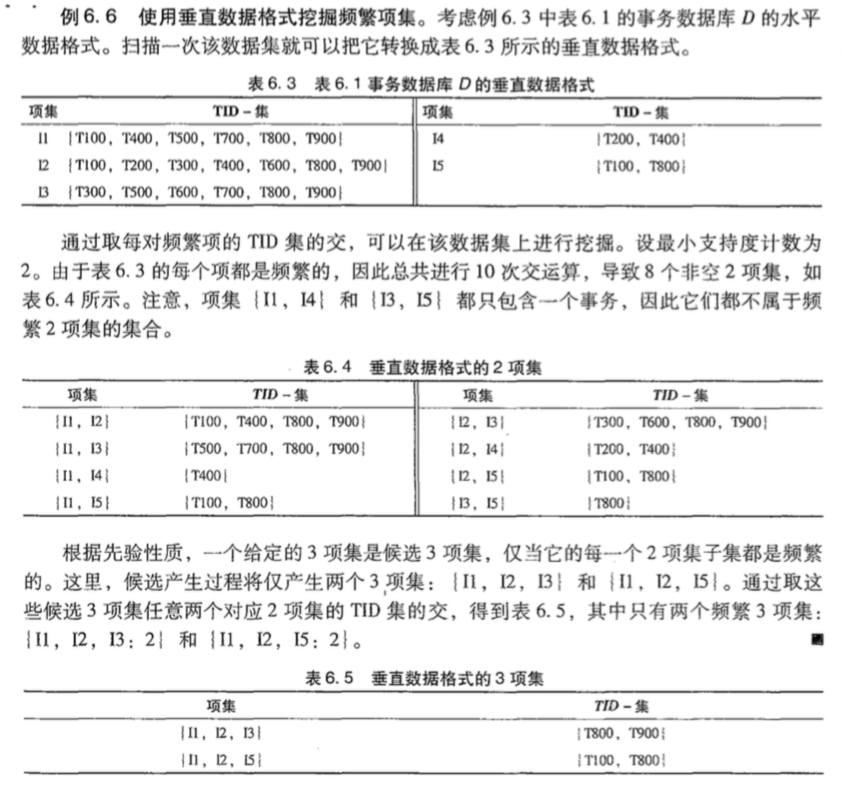
垂直数据格式挖掘频繁项集
上面的两种方法(Apriori和FP-Growth)都是水平数据格式的,垂直格式指的是每个项对应的事务ID。示例如下:
3.算法实现
这部分很久之前看《机器学习实战》的时候写过,直接放进来。
注意下面的Apriori代码里的关联规则部分只生成“A->B,A为单个item”的形式
Apriori
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Author: lxm
# @Date: 2015-11-12 16:34:51
# @Last Modified by: lxm
# @Last Modified time: 2015-11-15 19:39:49
import json
def loadDataSet():
return [[1,3,4],[2,3,5],[1,2,3,5],[2,5]]
def createC1(dataSet):
C1=[]
for line in dataSet:
for item in line:
if [item] not in C1:
C1.append([item])
return map(frozenset, C1)
def scanD(D,Ck,minSupport): #change Ck to Lk
support={}
for data in D:
for can in Ck:
if can.issubset(data):
if not support.has_key(can):
support[can]=1
else:
support[can]+=1
data_len=float(len(D))
retData=[]
supportRate={}
for can in support:
rate = support[can]/data_len
if rate>=minSupport:
retData.insert(0,can)
supportRate[can]=rate
return retData, supportRate
def createCk(Lk, k):
Ck=[]
length=len(Lk)
for i in range(length):
for j in range(i+1,length):
L1=list(Lk[i])[:k-2]
L2=list(Lk[j])[:k-2]
L1.sort()
L2.sort()
if L1==L2:
Ck.append((Lk[i]|Lk[j]))
return Ck
def apriori(dataSet, minSupport=0.5):
C1=createC1(dataSet)
D=map(set, dataSet)
L1, supportRate=scanD(D,C1,minSupport)
L=[]
L.append(L1)
k=2
while len(L[k-2])>2:
Ck=createCk(L[k-2], k)
Lk, Ratek=scanD(D,Ck,minSupport)
L.append(Lk)
supportRate.update(Ratek)
k+=1
return L, supportRate
def generateRules(L, supportRate, minConf=0.5):
bigRuleList = []
length=len(L)
for i in range(1,length):
for freqSet in L[i]:
H1=[frozenset([item]) for item in freqSet]
if i>1:
rulesFromConseq(freqSet, H1, supportRate, bigRuleList, minConf)
else:
calcConf(freqSet, H1, supportRate, bigRuleList, minConf)
return bigRuleList
def calcConf(freqSet, H1, supportRate, bigRuleList, minConf):
prunedH = []
for conseq in H1:
conf = supportRate[freqSet]/supportRate[freqSet-conseq]
if conf>=minConf:
print freqSet-conseq, "---->", conseq, ":", json.dumps([supportRate[freqSet], conf])
bigRuleList.append((freqSet-conseq,conseq,conf))
prunedH.append(conseq)
return prunedH
def rulesFromConseq(freqSet, H1, supportRate, bigRuleList, minConf):
length=len(H1[0])
if len(freqSet)>length+1:
newH=createCk(H1,length+1)
newH=calcConf(freqSet, newH, supportRate, bigRuleList, minConf)
if len(newH)>1:
rulesFromConseq(freqSet, newH, supportRate, bigRuleList, minConf)
if __name__ == '__main__':
# 1
# data = loadDataSet()
# C1=createC1(data)
# D=map(set, data)
# print D
# print C1
# retData, supportRate=scanD(D,C1,0.5)
# print retData
# print supportRate
# 2
# data = loadDataSet()
# L, supportRate = apriori(data, 0.7)
# print L
# print supportRate
# 3
# data = loadDataSet()
# L, supportRate = apriori(data)
# rule = generateRules(L,supportRate)
# print rule
# 4
# mushDataSet = [map(int,(line.strip().split())) for line in open('mushroom.dat')]
# L, supportRate =apriori(mushDataSet, 0.7)
# print L[1]
# 5
# data = ['MONKEY', 'DONKEY', 'MAKE', 'MUCKY', 'COOKIE']
# data = map(list, data)
# L, supportRate = apriori(data, 0.6)
# # print supportRate
# rule = generateRules(L, supportRate, 0.8)
# print rule
# 6
# data = [['Carb', 'Milk', 'Cheese', 'Bread'],
# ['Cheese', 'Milk', 'Apple', 'Pie', 'Bread'],
# ['Apple', 'Milk', 'Bread', 'Pie'],
# ['Bread', 'Milk', 'Cheese']]
# L, supportRate = apriori(data, 0.6)
# print L
# rule = generateRules(L, supportRate, 0.8)
# print rule
# 7
data = [['Kings', 'Sunset', 'Dairyland', 'Best'],
['Best', 'Dairyland', 'Goldenfarm', 'Tasty', 'Wonder'],
['Westcoast', 'Dairyland', 'Wonder', 'Tasty'],
['Wonder', 'Sunset', 'Dairyland']]
data2 = [['Carb', 'Milk', 'Cheese', 'Bread'],
['Cheese', 'Milk', 'Apple', 'Pie', 'Bread'],
['Apple', 'Milk', 'Bread', 'Pie'],
['Bread', 'Milk', 'Cheese']]
for i in range(len(data)):
for j in range(len(data[i])):
data[i][j] += data2[i][j]
print data
L, supportRate = apriori(data, 0.6)
print L
rule = generateRules(L, supportRate, 0.8)
print rule
FP-Growth
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Author: lxm
# @Date: 2015-11-16 13:49:44
# @Last Modified by: lxm
# @Last Modified time: 2015-11-16 16:25:27
class TreeNode:
def __init__(self, nameValue,numOccur, parentNode):
self.name=nameValue
self.count=numOccur
self.nodeLink=None
self.parent=parentNode
self.children={}
def inc(self, numOccur):
self.count+=numOccur
def disp(self, ind=1):
print " "*ind, self.name," ",self.count
for kid in self.children.values():
kid.disp(ind+1)
def createTree(dataSet, minSup):
headerTable={}
for data in dataSet:
for item in data:
headerTable[item]=headerTable.get(item,0)+dataSet[data]
for item in headerTable.keys():
if headerTable[item]<minSup:
del(headerTable[item])
freqItemSet=set(headerTable.keys())
if len(freqItemSet)==0:
return None,None
for k in headerTable.keys():
headerTable[k]=[headerTable[k],None]
retTree=TreeNode('Null Node', 1, None)
for data,count in dataSet.items():
localD={}
for item in data:
if item in freqItemSet:
localD[item]=headerTable[item][0]
if len(localD)>0:
curSortData=[a[0] for a in sorted(localD.items(), key=lambda p:p[1], reverse=True)]
updateTree(curSortData, retTree, headerTable, count)
return retTree, headerTable
def updateTree(items, inTree, headerTable, count):
if items[0] in inTree.children:
inTree.children[items[0]].inc(count)
else:
inTree.children[items[0]]=TreeNode(items[0],count,inTree)
if headerTable[items[0]][1]==None:
headerTable[items[0]][1]=inTree.children[items[0]]
else:
updateHeader(headerTable[items[0]][1], inTree.children[items[0]])
if len(items)>1:
updateTree(items[1:], inTree.children[items[0]], headerTable, count)
def updateHeader(firstNode, addNode):
while firstNode.nodeLink is not None:
firstNode=firstNode.nodeLink
firstNode.nodeLink=addNode
def loadSimpDat():
simpDat = [['r', 'z', 'h', 'j', 'p'],
['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],
['z'],
['r', 'x', 'n', 'o', 's'],
['y', 'r', 'x', 'z', 'q', 't', 'p'],
['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]
return simpDat
def createInitSet(dataSet):
retDict = {}
for trans in dataSet:
retDict[frozenset(trans)] = 1
return retDict
def ascendTree(leafNode,prefixPath):
if leafNode.parent!=None:
prefixPath.append(leafNode.name)
ascendTree(leafNode.parent, prefixPath)
def findPrefixPath(basePat, leafNode):
condPats={}
while leafNode is not None:
prefixPath=[]
ascendTree(leafNode, prefixPath)
if len(prefixPath)>1:
condPats[frozenset(prefixPath[1:])]=leafNode.count
leafNode=leafNode.nodeLink
return condPats
def mineTree(inTree, headerTable, minSup, preFix, freqItemList):
bigL = [v[0] for v in sorted(headerTable.items(), key=lambda p: p[1])]#(sort header table)
for basePat in bigL: #start from bottom of header table
newFreqSet = preFix.copy()
newFreqSet.add(basePat)
#print 'finalFrequent Item: ',newFreqSet #append to set
freqItemList.append(newFreqSet)
condPattBases = findPrefixPath(basePat, headerTable[basePat][1])
#print 'condPattBases :',basePat, condPattBases
#2. construct cond FP-tree from cond. pattern base
myCondTree, myHead = createTree(condPattBases, minSup)
#print 'head from conditional tree: ', myHead
if myHead != None: #3. mine cond. FP-tree
#print 'conditional tree for: ',newFreqSet
#myCondTree.disp(1)
mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)
if __name__ == '__main__':
# 1
# rootNode=TreeNode('first',10,None)
# rootNode2=TreeNode('second',9,None)
# rootNode.children['eye']=TreeNode('eye',8,None)
# rootNode.disp()
#
# 2
# simpDat = loadSimpDat()
# dataSet = createInitSet(simpDat)
# FPTree, headerTable = createTree(dataSet, 3)
# FPTree.disp()
# print headerTable
# 3
# simpDat = loadSimpDat()
# dataSet = createInitSet(simpDat)
# FPTree, headerTable = createTree(dataSet, 3)
# freqItems=[]
# mineTree(FPTree,headerTable,3,set([]),freqItems)
# 4
# simpDat = [line.strip().split() for line in open('kosarak.dat').readlines()]
# dataSet = createInitSet(simpDat)
# FPTree, headerTable=createTree(dataSet,100000)
# freqItems=[]
# mineTree(FPTree, headerTable,100000,set([]), freqItems)
# print freqItems
# 5
import time
t1 = time.time()
data = ['MONKEY', 'DONKEY', 'MAKE', 'MUCKY', 'COOKIE']
data = map(list, data)
dataSet = createInitSet(data)
FPTree, headerTable = createTree(dataSet, 3)
freqItems = []
mineTree(FPTree, headerTable, 3, set([]), freqItems)
print time.time()-t1
print freqItems
4.兴趣度量——模式评估方法
除了置信度和支持度之外,还需要考虑一些用户感兴趣的规则,比如相关度量等。
相关度量
提升度
对两个频繁项集A和B,提升度公式如下:
\[lift(A,B)=\frac{P(A{\bigcup}B)}{P(A)P(B)}\]当提升度小于1,则A的出现和B的出现是负相关的;当提升度大于1,则A的出现和B的出现是正相关的。当提升度等于1,则A和B是独立的。
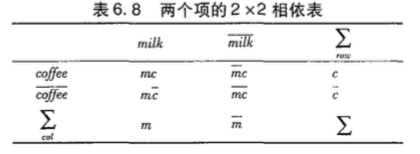
$\chi^2$值
\[\chi^2=\sum{\frac{(观测-期望)^2}{期望}}\]由于上述两个相关度量和零事务相关,容易收到零事务的影响,因此有时候这两个度量的表现会很差,因此我们推荐使用下面的评估模式,对相关性进行度量。
零事务即$\bar{A}\bar{B}$的个数,表明A和B都不出现。这部分是用户不感兴趣的,应该刨除这部分的影响。
其他评估模式
全置信度(all_confidence)
\[all\_conf(A,B)=\frac{sup(A{\bigcup}B)}{max\{sup(A),sup(B)\}}=min\{P(A|B),P(B|A)\}\]最大置信度(max_confidence)
\[max\_conf(A,B)=min\{P(A|B),P(B|A)\}\]Kulczynski
\[Kulc(A,B)=\frac12(P(A|B)+P(B|A))\]余弦
\[cosine(A,B)=\sqrt{(P(A|B){\times}P(B|A))}\]以上四个度量仅仅和两个条件概率有关,并且都在0到1范围。且具有以下性质:
- 大于0.5为正相关
- 小于0.5为负相关
- 等于0.5为中立
不平衡比
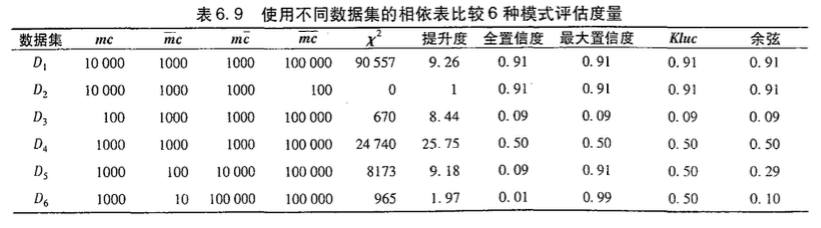
虽然上述的度量虽然和零事务都没关系(零不变性,上述6种相关度量只有提升度和卡方值不具有零不变性),但是各个度量的效果却不相同,如下面的例子中,D5和D6的Kluc判定m和c为中立的,而余弦度量和全置信度认为负相关,最大置信度认为正相关。
这样,则需要引入不平衡比来衡量两个项集的不平衡程度。
\[IR(A,B)=\frac{|sup(A)-sup(B)|}{sup(A)+sup(B)-sup(A{\bigcup}B)}\]IR值越大,说明越不平衡。一般结合IR和上述四种度量来衡量项集的相关性。
5.参考
- 《Machine Learning in Action》
- 《数据挖掘:概念与基础(中文第三版)》
- MLinAction所有代码
- Apriori代码和数据
- FP-Growth代码和数据