树结构算法总结(1) 二叉树的遍历
1.非递归的遍历
前序遍历
思路
使用栈来模拟,比较简单,直接上代码。
代码
/**
* Definition of TreeNode:
* class TreeNode {
* public:
* int val;
* TreeNode *left, *right;
* TreeNode(int val) {
* this->val = val;
* this->left = this->right = NULL;
* }
* }
*/
class Solution {
public:
/**
* @param root: The root of binary tree.
* @return: Preorder in vector which contains node values.
*/
vector<int> preorderTraversal(TreeNode *root) {
// write your code here
stack<TreeNode*> q;
vector<int> res;
TreeNode* cur = root;
while(cur){
res.push_back(cur->val);
q.push(cur);
cur = cur->left;
}
while(!q.empty()){
TreeNode* cur = q.top();
q.pop();
if(cur->right){
cur = cur->right;
while(cur){
res.push_back(cur->val);
q.push(cur);
cur = cur->left;
}
}
}
return res;
}
};
中序遍历
思路
同样用栈模拟,对比前序遍历稍作修改即可。
代码
/**
* Definition of TreeNode:
* class TreeNode {
* public:
* int val;
* TreeNode *left, *right;
* TreeNode(int val) {
* this->val = val;
* this->left = this->right = NULL;
* }
* }
*/
class Solution {
/**
* @param root: The root of binary tree.
* @return: Inorder in vector which contains node values.
*/
public:
vector<int> inorderTraversal(TreeNode *root) {
// write your code here
stack<TreeNode*> s;
vector<int> res;
TreeNode* cur = root;
while(cur){
s.push(cur);
cur = cur->left;
}
while(!s.empty()){
TreeNode* cur = s.top();
s.pop();
res.push_back(cur->val);
cur = cur->right;
while(cur){
s.push(cur);
cur = cur->left;
}
}
return res;
}
};
扩展——二叉查找树迭代器
二叉查找树是用于查找的平衡二叉排序树。可以使用中序遍历的思路来按顺序(数值的大小)访问节点。
代码如下:
/**
* Definition of TreeNode:
* class TreeNode {
* public:
* int val;
* TreeNode *left, *right;
* TreeNode(int val) {
* this->val = val;
* this->left = this->right = NULL;
* }
* }
* Example of iterate a tree:
* BSTIterator iterator = BSTIterator(root);
* while (iterator.hasNext()) {
* TreeNode * node = iterator.next();
* do something for node
*/
class BSTIterator {
public:
stack<TreeNode*> s;
//@param root: The root of binary tree.
BSTIterator(TreeNode *root) {
// write your code here
while(root){
s.push(root);
root = root->left;
}
}
//@return: True if there has next node, or false
bool hasNext() {
// write your code here
return !s.empty();
}
//@return: return next node
TreeNode* next() {
// write your code here
TreeNode* cur = s.top();
s.pop();
TreeNode* tmp = cur;
tmp = tmp->right;
while(tmp){
s.push(tmp);
tmp = tmp->left;
}
return cur;
}
};
后序遍历
思路
同样使用栈来模拟,不过要考虑的顺序是左、右、中。首先存储树的左边节点,之后判定最后一个左节点是否有右节点,如果有的话先对该右节点做上面同样的操作;如果没有右节点或者右节点被访问过,则访问当前节点,并将该节点从栈中删除。
代码
/**
* Definition of TreeNode:
* class TreeNode {
* public:
* int val;
* TreeNode *left, *right;
* TreeNode(int val) {
* this->val = val;
* this->left = this->right = NULL;
* }
* }
*/
class Solution {
/**
* @param root: The root of binary tree.
* @return: Postorder in vector which contains node values.
*/
public:
vector<int> postorderTraversal(TreeNode *root) {
// write your code here
vector<int> res;
stack<TreeNode*> s;
while(root){
s.push(root);
root = root->left;
}
TreeNode* pre = NULL;
while(!s.empty()){
TreeNode* cur = s.top();
if(!cur->right||cur->right==pre){
res.push_back(cur->val);
pre = cur;
s.pop();
}
else{
cur = cur->right;
while(cur){
s.push(cur);
cur = cur->left;
}
}
}
return res;
}
};
层序遍历
思路
使用队列来模拟。如果要区别每层的元素有哪些,则需要使用一个变量来存储每层的个数,比如一开始第一层只有一个根节点,故size=1。访问过第一层后,size=0,之后更新第二层size=queue.size(),即之前通过第一层访问后产生的所有左右节点的个数,即为第二层。同理,以此类推。
代码
/**
* Definition of TreeNode:
* class TreeNode {
* public:
* int val;
* TreeNode *left, *right;
* TreeNode(int val) {
* this->val = val;
* this->left = this->right = NULL;
* }
* }
*/
class Solution {
/**
* @param root: The root of binary tree.
* @return: Level order a list of lists of integer
*/
public:
vector<vector<int>> levelOrder(TreeNode *root) {
// write your code here
vector<vector<int>> res;
queue<TreeNode*> q;
// if(root==NULL)
// return res;
q.push(root);
TreeNode* cur;
int size = 0;
vector<int> tmp;
while(!q.empty()){
cur = q.front();
if(size==0)
size = q.size();
q.pop();
if(cur!=NULL){
q.push(cur->left);
q.push(cur->right);
tmp.push_back(cur->val);
}
size--;
if(!q.empty()&&size==0){
res.push_back(tmp);
tmp.clear();
}
}
return res;
}
};
2.通过遍历构造树
这块我们统一使用一样的例子,其树结构如下:
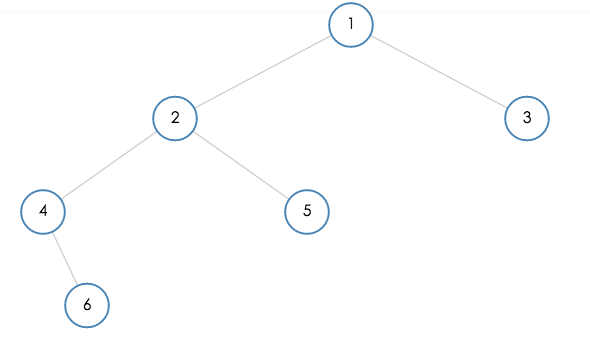
这棵树的各个遍历如下
前序遍历:[1,2,4,6,5,3]
中序遍历:[4,6,2,5,1,3]
后序遍历:[6,4,5,2,3,1]
已知前序遍历和中序遍历,构造二叉树
思路
考虑递归结构,我们每次都只构造一个子树。
- 前序遍历的顺序可以看作root->left->right,所以我们总是能够从前序遍历里轻易找到子树的root节点(树的根节点为第一个元素),左子树根节点即为当前root+1,而右子树根节点为root+len(left),len(left)可以通过中序遍历找到。
- 而中序遍历的顺序可以看作left->root->right,所以我们总是能够通过前序的根节点值找到中序的根节点位置,然后得到左子树和右子树。
总的来说,前序遍历找根节点,中序遍历找左右子树。
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int len = preorder.size();
if(len<1)
return NULL;
return build(preorder, inorder, 0, len-1, 0);
}
TreeNode* build(vector<int>& preorder, vector<int>& inorder, int l, int r, int root){
if(l>r)
return NULL;
TreeNode* cur = new TreeNode(preorder[root]);
int pos = l;
while(preorder[root]!=inorder[pos])pos++;
cur->left = build(preorder, inorder, l, pos-1, root+1);
cur->right = build(preorder, inorder, pos+1, r, pos+1+root-l);
return cur;
}
};
非递归的方法
思路:其实可以考虑从根节点出发,先将所有左节点存入栈中,之后通过中序遍历判定最后一个左节点是否存在右孩子(不存在的话,那么此时栈顶元素的值等于当前中序遍历的值),如果没有,则回溯(pop),直到找到有右孩子的节点为止。比如上面的例子中:
前序遍历:a=[1,2,4,6,5,3]
中序遍历:b=[4,6,2,5,1,3]
一开始存入栈中的有[1,2,4],此时栈顶元素4==b[0],则pop出4,之后再判定4之后的6是否是栈顶元素,即2!=6==b[1],所以此时6为4的右孩子,将其存入栈中。
如果删除元素6,则:
前序遍历:a=[1,2,4,5,3]
中序遍历:b=[4,2,5,1,3]
一开始存入栈中的有[1,2,4],此时栈顶元素4==b[0],则pop出4,之后再判定4之后的2是否是栈顶元素,即2==2==b[1],所以此时4没有右子树,再回溯到2继续判断2是否有右子树,直接把2再pop出去,再判定栈顶元素1,可知1!=5==b[3],所以5是2的右孩子,将其存入栈中。
如此对前序遍历循环即可求解。
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int len = preorder.size();
if(len<1)
return NULL;
stack<TreeNode*> s;
int i = 1, j = 0;
TreeNode* root = new TreeNode(preorder[0]);
s.push(root);
for(;i<len;i++){
TreeNode* cur = s.top();
if(cur->val==inorder[j]){
while(!s.empty()&&s.top()->val==inorder[j]){
cur = s.top();
s.pop();
j++;
}
if(i<len){
cur->right = new TreeNode(preorder[i]);
s.push(cur->right);
}
}
else{
cur->left = new TreeNode(preorder[i]);
s.push(cur->left);
}
}
return root;
}
已知中序遍历和后序遍历,构造二叉树
思路
后序遍历顺序为left->right->root,如果反过来,则是root->right->left,之后的用法和上面类似,只不过左右对调了。
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
int len = inorder.size();
if(len<1)
return NULL;
return build(inorder, postorder, 0, len-1, len-1);
}
TreeNode* build(vector<int>& inorder, vector<int>& postorder, int l, int r, int root){
if(l>r)
return NULL;
TreeNode* cur = new TreeNode(postorder[root]);
int pos = l;
while(inorder[pos]!=postorder[root])pos++;
cur->left = build(inorder, postorder, l, pos-1, root-r+pos-1);
cur->right = build(inorder, postorder, pos+1, r, root-1);
return cur;
}
};
非递归的方法
思路:和上面的一样,只不过是要倒过来(同时把中序和后序倒过来,左右子树也要再反一下)
class Solution {
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
int len = inorder.size();
if(len<1)
return NULL;
stack<TreeNode*> s;
int i = len-2,j = len-1;
TreeNode* root = new TreeNode(postorder[len-1]);
s.push(root);
for(;i>=0;i--){
TreeNode* cur = s.top();
if(cur->val==inorder[j]){
while(!s.empty()&&s.top()->val==inorder[j]){
cur = s.top();
s.pop();
j--;
}
if(j>=0){
cur->left = new TreeNode(postorder[i]);
s.push(cur->left);
}
}
else{
cur->right = new TreeNode(postorder[i]);
s.push(cur->right);
}
}
return root;
}
注:不能够通过前序和后序构造,因为前序和后序是等价的,只能够区分根节点和非根节点,无法区分左右子树。