VAE模型
什么是VAE
当我们谈论GAN的时候,往往会把VAE也一并拿出来说。在生成模型方面,这两个算是目前的大热门(尤其是GAN)。那么VAE究竟是什么呢?作为一个生成模型,它首先需要具备生成样本的能力(从$P(X)$分布中采样得到)。
Variational Autoencoder(VAE)从名字上看,是由变分+自动编码器组成,不过它与我们所熟悉的Autoencoder还不一样,只是在模型结构上借鉴了encoder和decoder的思路。并且,这两部分的作用也不同,在autoencoder中,encoder用来对输入数据压缩编码,decoder则还原为原来的数据;而在VAE中,encoder将输入数据$x$“压缩”为隐变量$z$,decoder将隐变量“重构”为新的样本。
经过了以上的介绍,相信大家对VAE有一个初步的认识。那么,接下来就是如何去构建这个网络(哪里用模型、哪里假设分布、损失函数用什么)。
VAE与AE不同,AE虽然也是无监督学习,但它并不是一个生成模型,不具备泛化能力。当VAE中的$\sigma^2$为0时,表明随机变量$z$是一个确定性变量($z=\mu$),那么,此时VAE就变成了AE。
现在,我们根据VAE的模型图,尝试从“常识”与“假设”上直接得到VAE的目标函数。假设图中的$\tilde x = y$。
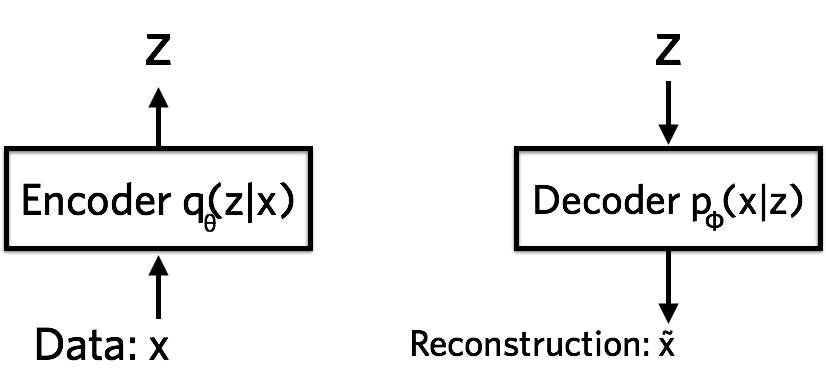
上面的loss function是针对一个样本而言的。其中,$\theta$与$\phi$就是我们需要学习的分布的参数。从公式可以看到,损失函数分为两部分:前面的部分为KL散度,它表示隐变量分布与我们想要的真实分布之间的差异;后面的部分表示decoder层通过隐变量得到样本的对数概率关于$q_{\phi}(z \mid x^{(i)})$均值。
左侧公式
假设$q_{\phi}(z \mid x^{(i)}) \sim \mathcal{N}(\mu, {\sigma^2})$,$p_{\theta}(z) \sim \mathcal{N}(0, 1)$,则左侧的KL散度可以写成:
\[\begin{align} &KL(q_{\phi}(z \mid x^{(i)}) \parallel p_{\theta}(z)) \\ =&KL(\mathcal{N}(\mu^{(i)}, (\sigma^{(i)})^2) \parallel \mathcal{N}(0, 1)) \\ =&\int\frac{1}{\sqrt{2\pi(\sigma^{(i)})^2}}e^{-(x^{(i)}-\mu^{(i)})^2/2(\sigma^{(i)})^2} \left(\log \frac{e^{-(x^{(i)}-\mu^{(i)})^2/2(\sigma^{(i)})^2}/\sqrt{2\pi(\sigma^{(i)})^2}}{e^{({-x^{(i)})^2}/2}/\sqrt{2\pi}}\right)dx^{(i)} \\ =&\frac{1}{2}\Big(-\log(\sigma^{(i)})^2+(\mu^{(i)})^2+(\sigma^{(i)})^2-1\Big) \end{align}\]右侧公式
对于右侧的公式,假设最后输出的是二值图像(每个像素点为0或1),则$p_{\theta}(x^{(i)} \mid z)$可以是伯努利分布,如果是连续值图像,则可以是高斯分布。
伯努利分布
考虑x的每个像素点为$x_k$,输出的每个像素点预测概率为$y_k$,则右侧对应交叉熵损失:
\[p_{\theta}(x \mid z)=\Pi_{k=1}^{D}y_k(z)^{x_k}(1-y_k(z))^{1-x_k} \\ \\ logp_{\theta}(x \mid z)=\Sigma_{k=1}^{D}(x_k*logy_k(z)+(1-x_k)*log(1-y_k(z)))\]高斯分布
同考虑x的每个像素点为$x_k$,则:
\[p_{\theta}(x \mid z)=\frac{1}{\prod\limits_{k=1}^D \sqrt{2\pi \sigma^2(z)}}\exp\left(-\frac{1}{2}\left\Vert\frac{x_k-\mu(z)}{\sigma(z)}\right\Vert^2\right) \\ \\ logp_{\theta}(x \mid z)=-\left(\frac{1}{2}\left\Vert\frac{x_k-\mu(z)}{\sigma(z)}\right\Vert^2\right)-\frac{1}{2}\Sigma_{k=1}^{D}log\sigma^2(z)-C\]当$\sigma(z)=\sigma$时,右侧公式对应MSE。
VAE的推导
第一部分为我们说明了VAE的一个直观的认识。那么从第一部分直接冒出来的损失函数是怎么得到的呢?
首先,考虑输入样本是独立同分布的,那么对于每个样本,我们希望通过decoder部分后验概率$q_{\phi}(z|x^{(i)})$去拟合真实的后验概率分布$p_{\theta}(x^{(i)}|z)$,那么我们希望$q$对$p$的KL散度要尽量小,于是有:
由上面可知,要极大化边缘分布$p(X)$,可以直接通过减少变分下界$L(\phi,\theta;x^{(i)})$,而它的变分下界就是我们上面要求的目标函数(损失函数)。
VAE神经网络模型结构
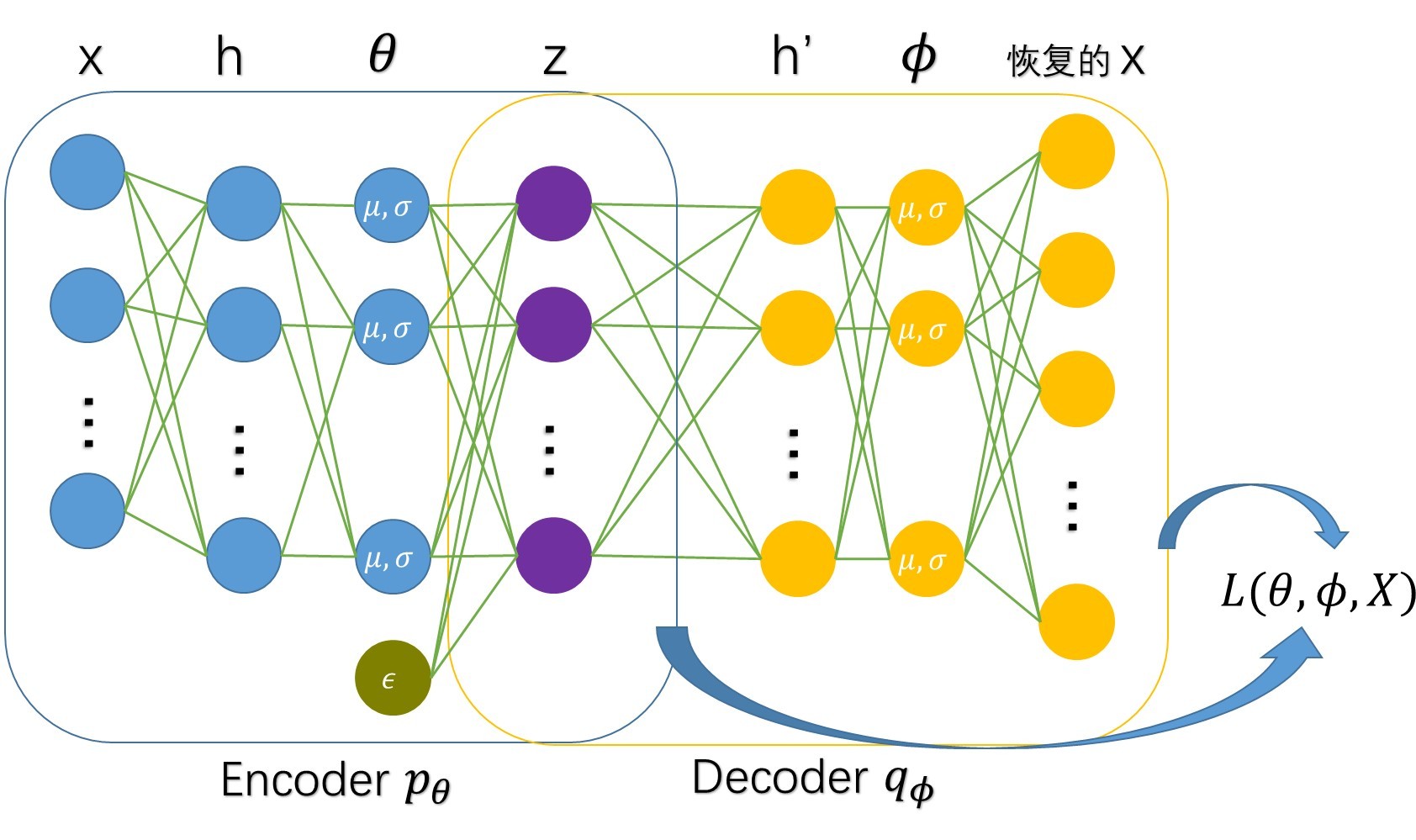
Encoder
输入x(如图像),经过两个神经网络(h),分别得到$p_{\theta}$的分布参数$\mu$与$log\sigma^2$(之所以预测$log\sigma^2$而不是$\sigma^2$的原因是$\sigma^2>=0$,而$log\sigma^2$可正可负),之后通过$\epsilon$采样后计算$z=\mu+\sigma \odot \epsilon$。
Decoder
直接将Encoder得到的隐变量$z$经过神经网络,得到输出值(如果是离散的,则可以经过softmax进行预测,最后计算cross entropy;否则可以直接算MSE)。
Reparameterization Trick
由于encoder直接输出隐变量$z$的采样值,如果用encoder用神经网络来模拟,那么无法通过BP训练(随机采样无法求导),因此需要用一点小技巧。首先我们通过神经网络得到$p_{\theta}$参数$\theta=(\mu,log\sigma^2)$,然后通过变换$z=\mu+\sigma \odot \epsilon,\epsilon \sim \mathcal{N}(0,1)$,这样,在梯度回传的时候,可以直接更新网络。
小小实验
接下来,我们通过mnist数据集实验,来观察VAE的生成效果,而且不像GAN,我们可以直接通过一个指标(loss)来监督训练过程。
下面通过两个版本来实现VAE,实现过程差异不大,有兴趣的读者可以尝试自己按照上面的公式写一遍。具体代码地址如下:
code for VAE
keras版本
epoch=5时,z的分布(实验中z为二维),不同颜色代表不同数字类别,此时z已经有些标准正态分布的样子了,但是方差依然比较大:
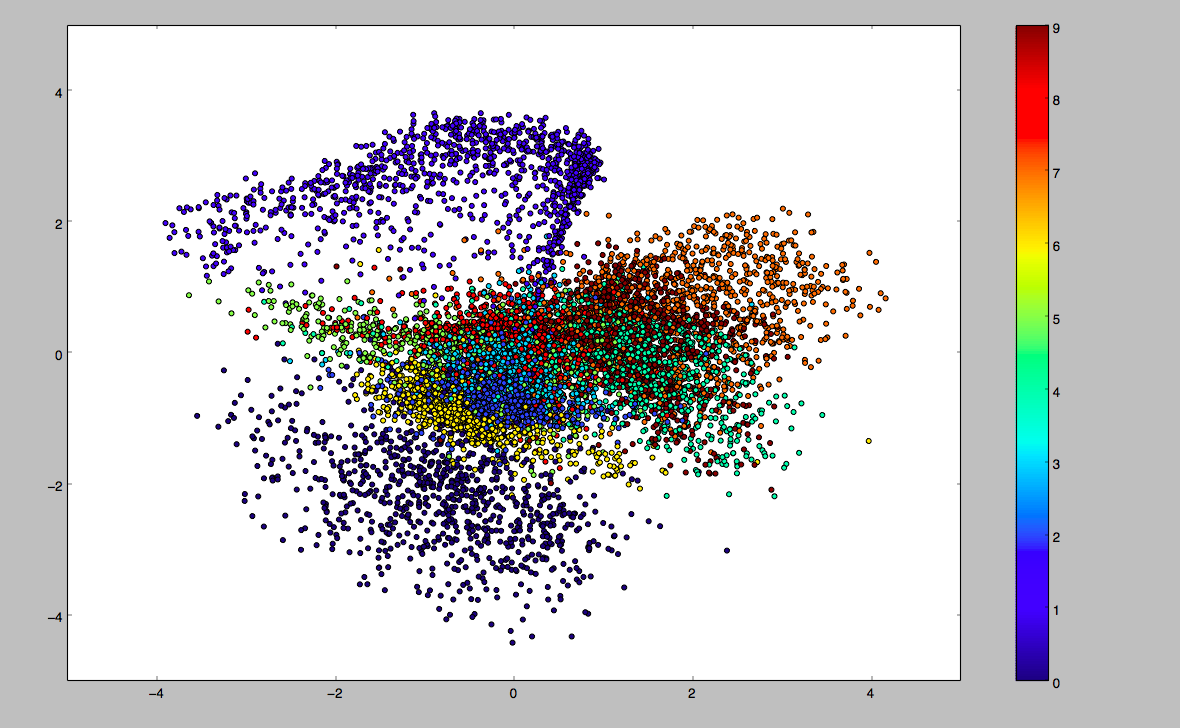
epoch=5时,generator(decoder)的输出,可见效果还比较普通:

epoch=50时,z的分布(实验中z为二维),不同颜色代表不同数字类别,每个类别学习到了它自身的分布特征(虽然我们没有给类别标签,但是不同类别的样本还是有显著差异的),每种数字能形成一个簇:
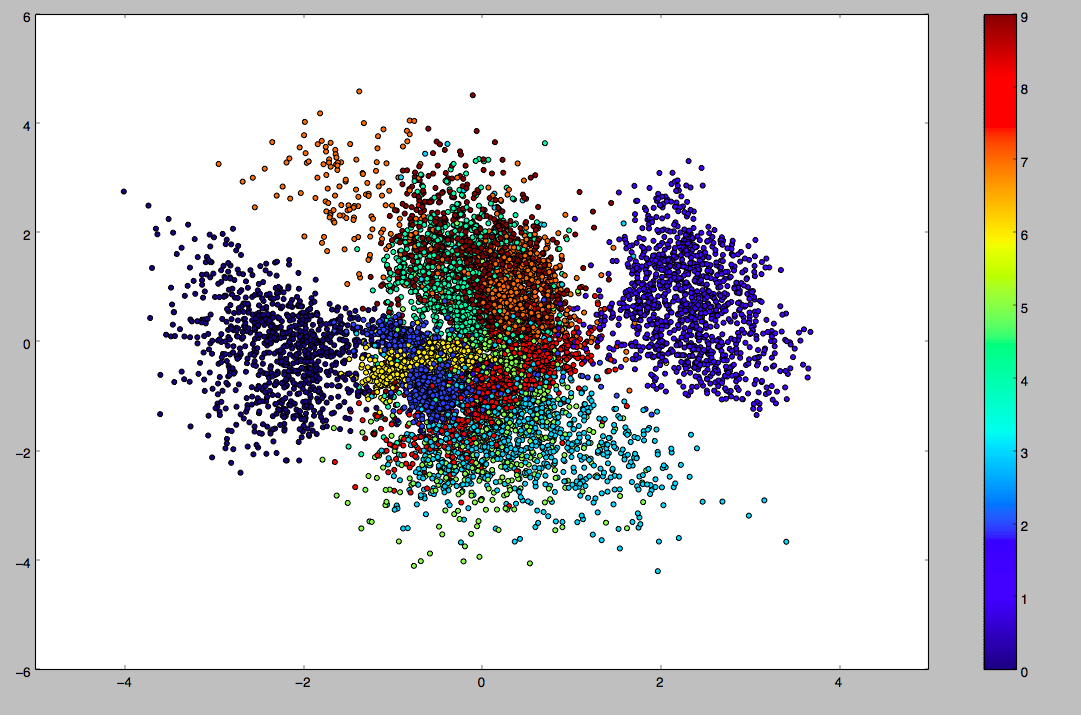
epoch=50时,generator(decoder)的输出,效果比epoch=5时要好一些:

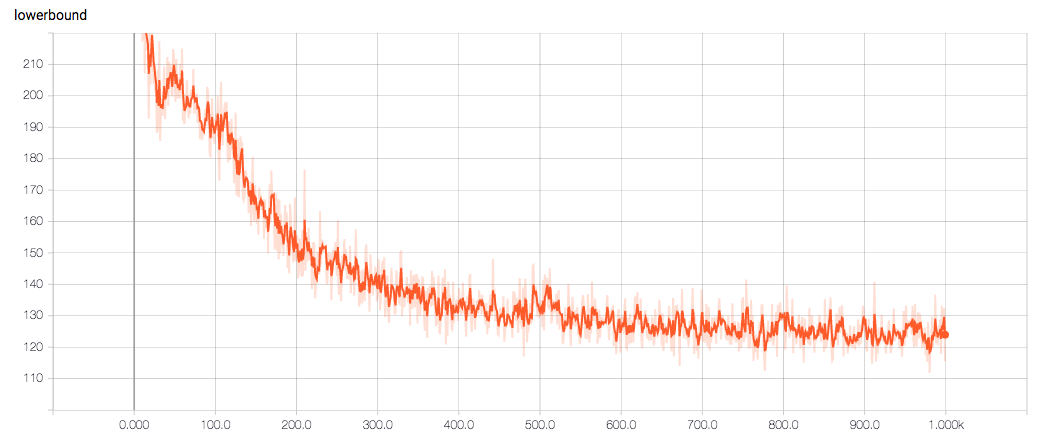
tensorflow版本
训练1000个step,training loss如下: