Clustering杂谈
聚类算法有很多,主要的目标就是将一堆数据中相似的数据归到一起,而不去管这个数据的具体标签。归类的方法直接从数据点中获取,在机器学习上这种方法属于非监督学习(Unsupervised Learning)。
常用的聚类算法,比较经典的有k-means、k-medoids、GMM等。比较现代和流行的是Spectral Clustering(谱聚类)和Hierarchical Clustering(层级聚类)。
本节用的例子数据地址:
直接复制粘贴即可。
所有代码地址:
1.k-means
k均值聚类的思路比较清晰,就是给每个数据分配一个具体的标签。使用k均值聚类需要事先确定聚类数。
k-means的算法步骤如下:
- 选定$K$个中心$\mu_k$的初值。这个过程通常是针对具体的问题有一些启发式的选取方法,或者大多数情况下采用随机选取的办法。因为前面说过k-means并不能保证全局最优,而是否能收敛到全局最优解其实和初值的选取有很大的关系,所以有时候我们会多次选取初值跑k-means,并取其中最好的一次结果。
- 将每个数据点归类到离它最近的那个中心点所代表的cluster中。 用公式$\mu_k = \frac{1}{N_k}\sum_{j\in\text{cluster}_k}x_j $计算出每个cluster的新的中心点。
- 重复第二步,一直到迭代了最大的步数或者前后的总误差$J$的值相差小于一个阈值为止。其中总误差$J$的公式如下:
- $\displaystyle J = \sum_{n=1}^N\sum_{k=1}^K r_{nk} |x_n-\mu_k|^2$
k-means的迭代过程其实是简化的EM算法思想。
代码
# -*- encoding:utf-8 -*-
import numpy as np
from matplotlib import pyplot as plt
import pickle
from copy import deepcopy
import random
class Kmeans():
def __init__(self, k=3, filepath='../data/cluster.pkl'):
self.samples = self.loadData(filepath)
# K个聚类点component
self.K = k
# 数据预处理
self.random_points = np.zeros([len(self.samples)*len(self.samples[0][0]), 2])
i = 0
for smp in self.samples:
smp_len = len(smp[0])
self.random_points[i:i+smp_len,0] = smp[0]
self.random_points[i:i+smp_len,1] = smp[1]
i += smp_len
# M条数据,每条数据N个特征
self.M, self.N = self.random_points.shape
self.centroids = self.initial(self.K)
self.dist = np.zeros((self.M, self.K))
# 加载数据
def loadData(self, filepath):
with open(filepath) as fr:
return pickle.load(fr)
# k均值
def kmeans(self, K, all=None):
# 初始化中心点
centroids = self.initial(K, all)
if not all:
all = range(0, self.M)
dist = deepcopy(self.dist)
cost = np.inf
# 循环终止门限
threshold = 1e-3
while True:
cur_cost = 0.
# 计算每个点到当前各个聚类点的距离
for k in range(K):
dist[all,k] = np.sqrt(np.sum(np.power(self.random_points[all,:]-centroids[k], 2), 1))
# 更新中心点
for k in range(K):
all_ind = np.argmin(dist, 1)
k_ind = (all_ind == k).nonzero()[0]
k_ind = list((set(all) & set(k_ind)))
k_points = self.random_points[k_ind,:]
centroids[k] = np.average(k_points, 0)
cur_cost += np.sum(dist[k_ind, k])
print cur_cost
# 如果收敛,则跳出循环
if abs(cur_cost-cost)<threshold:
break
cost = cur_cost
# self.centroids = centroids
# self.dist = dist
return dist, centroids
def initial(self, K, all=None):
if not all:
return self.random_points[np.random.choice(range(0,self.M), K, replace=False)]
else:
return self.random_points[np.random.choice(all, K, replace=False)]
def draw(self, dist):
plt.figure(1)
all_ind = np.argmin(dist, 1)
color = ['r', 'g', 'b']
for k in range(self.K):
x, y = self.random_points[(all_ind==k).nonzero()[0],0],self.random_points[(all_ind==k).nonzero()[0],1]
plt.scatter(x, y , c=color[k])
plt.show()
if __name__ == '__main__':
km = Kmeans()
dist, centroids = km.kmeans(3)
km.draw(dist)
结果
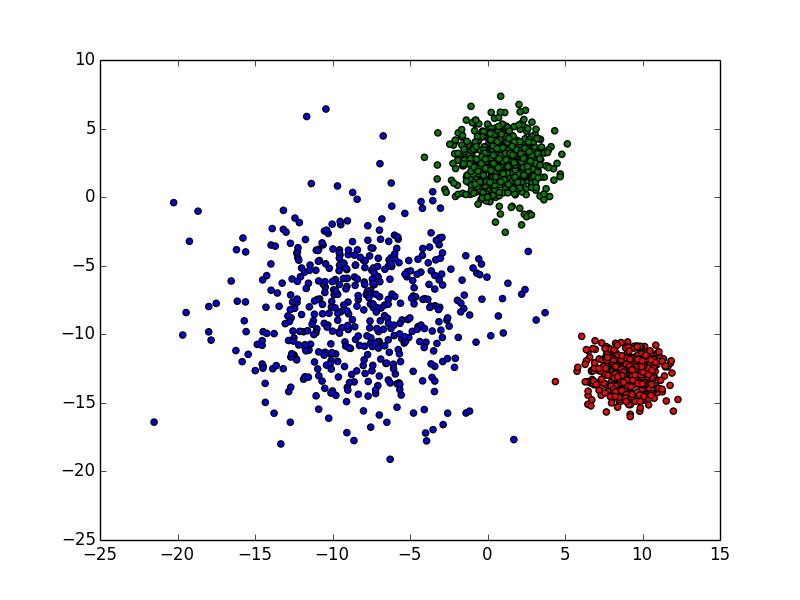
原数据
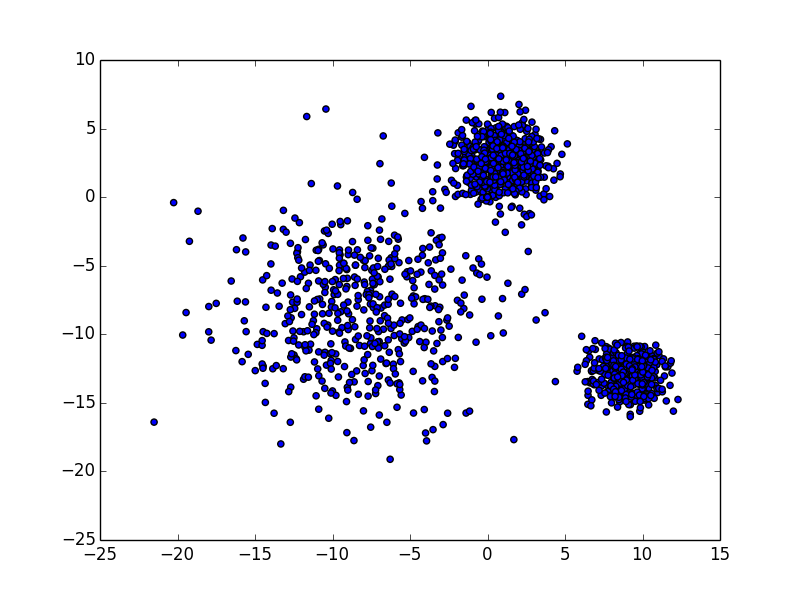
聚类结果
二分k-means
关于k-means的变种,还有二分k-means。二分k-means的算法步骤如下:
- 将所有数据点看成一个簇(初始化的簇位置为所有点的均值)。
- 对每一个簇,计算该簇的总误差,并对该簇进行k-均值聚类(k=2),计算将该簇一分为二后的总误差和。误差可以是簇中所有点到簇的聚类点的平均距离
- 选择使得误差最小的那个簇进行划分操作。
- 循环2到3,知道簇的数目为k为止。
二分k-means代码
# -*- encoding:utf-8 -*-
import numpy as np
from matplotlib import pyplot as plt
import pickle
from copy import deepcopy
import random
class Kmeans():
def __init__(self, k=3, filepath='../data/cluster.pkl'):
self.samples = self.loadData(filepath)
# K个聚类点component
self.K = k
# 数据预处理
self.random_points = np.zeros([len(self.samples)*len(self.samples[0][0]), 2])
i = 0
for smp in self.samples:
smp_len = len(smp[0])
self.random_points[i:i+smp_len,0] = smp[0]
self.random_points[i:i+smp_len,1] = smp[1]
i += smp_len
# M条数据,每条数据N个特征
self.M, self.N = self.random_points.shape
# 加载数据
def loadData(self, filepath):
with open(filepath) as fr:
return pickle.load(fr)
# k均值
def kmeans(self, K, all=None):
centroids = self.initial(K, all)
if all is None:
all = range(0, self.M)
all = np.array(all)
dist = np.zeros([len(all), K])
cost = np.inf
threshold = 1e-3
while True:
cur_cost = 0.
split_parts = list()
split_cost = list()
split_dist_ind = list()
for k in range(K):
dist[:,k] = np.sqrt(np.sum(np.power(self.random_points[all,:]-centroids[k], 2), 1))
for k in range(K):
all_ind = np.argmin(dist, 1)
dist_ind = (all_ind==k).nonzero()[0]
k_ind = all[dist_ind]
split_parts.append(k_ind)
k_points = self.random_points[k_ind,:]
centroids[k] = np.average(k_points, 0)
cur_cost += np.sum(dist[dist_ind, k])
split_cost.append(np.sum(dist[dist_ind, k]))
split_dist_ind.append(dist_ind)
print cur_cost
if abs(cur_cost-cost)<threshold:
break
cost = cur_cost
del split_parts
del split_cost
# self.centroids = centroids
# self.dist = dist
return dist, centroids, split_parts, cur_cost, split_cost
def bikmeans(self, K):
# 簇的数量
cur_num = 1
# 各个簇的聚类点
centroids = [list(np.average(self.random_points, 0))]
# 各个簇的cost
cost = [np.sum(np.sqrt(np.sum(np.power(self.random_points-centroids[0], 2), 1)))]
# 各个簇的数据样本ID
all = [range(0, self.M)]
# 对于K个聚类点,进行K-1次划分
for _ in range(K-1):
min_cost = np.inf
# 对每个簇进行遍历更新
for i in range(cur_num):
# 当前簇的聚类点(2个),划分的数据,划分前的cost,划分后的cost
_, cur_centroids, split_parts, cur_cost, split_cost = self.kmeans(2, all[i])
if i == 0 or cost[i]-cur_cost > cost[min_ind]-min_cost:
min_cost = cur_cost
min_ind = i
min_centroids = cur_centroids
min_split_cost = split_cost
min_split_parts = split_parts
centroids[min_ind] = min_centroids[0]
centroids.append(min_centroids[1])
all[min_ind] = min_split_parts[0]
all.append(min_split_parts[1])
cost[min_ind] = min_split_cost[0]
cost.append(min_split_cost[1])
cur_num += 1
return all
def initial(self, K, all=None):
if all is None:
return self.random_points[np.random.choice(range(0,self.M), K, replace=False)]
else:
return self.random_points[np.random.choice(all, K, replace=False)]
def drawBiKmeans(self, points):
plt.figure(1)
color = ['r', 'g', 'b']
for k in range(self.K):
x, y = self.random_points[points[k],0],self.random_points[points[k],1]
plt.scatter(x, y , c=color[k])
plt.show()
if __name__ == '__main__':
km = Kmeans()
points = km.bikmeans(3)
km.drawBiKmeans(points)
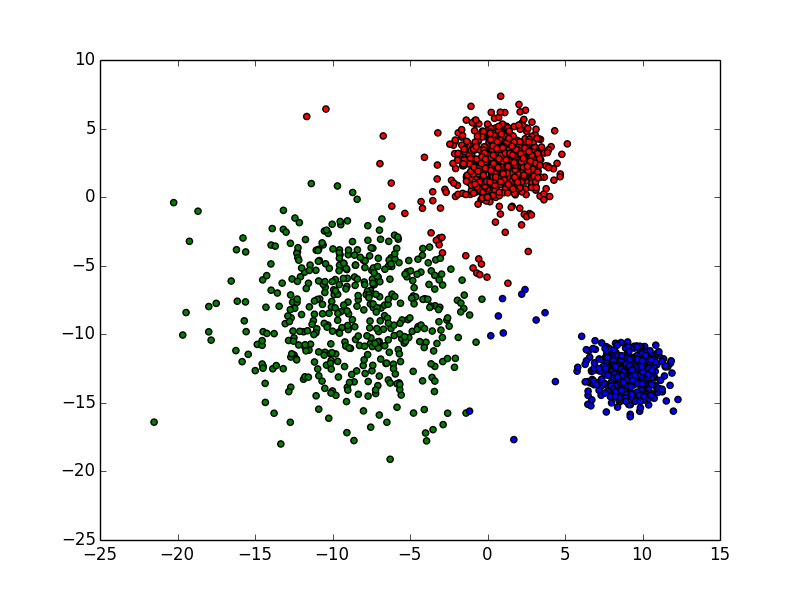
二分kmeans结果
2.k-medoids
k均值的簇坐标为所有簇点的均值(means),而k-medoids则是选取簇中存在的点,该点是距离同个簇的所有其他点距离和最小的点,即寻找中位数(medium)。
k-medoids对于聚类点的选取要求没有k-means高,因此k-means能做的k-medoids也能做。k-medoids主要针对的是非数字化特征的数据,每个样本点之间只有一个差异度值。那么我们就可以构造一个距离矩阵(N*K),相应的误差公式如下:
$\mathcal{V}(x_n,\mu_k)$表示数据点到中心点的距离。而$r_{nk}$表示该数据点n是否在中心点k的簇里,是为1,否则为0。
可以看到k-means只要求得簇点均值即可,复杂度为O(N)。而k-medoids则要计算簇中每个点到其他点的距离,复杂度为O(N^2)。但是由于k-medoids找的是已有的点,它不会像k-means一样产生离群(outlier)的聚类点,也不会选择数据中的离群点为聚类点,因此k-medoids比k-means要更具健壮(robust)。
代码
# -*- encoding:utf-8 -*-
import numpy as np
from matplotlib import pyplot as plt
import pickle
from copy import deepcopy
import random
class Kmeans():
def __init__(self, k=3, filepath='../data/cluster.pkl'):
self.samples = self.loadData(filepath)
# K个聚类点component
self.K = k
# 数据预处理
self.random_points = np.zeros([len(self.samples)*len(self.samples[0][0]), 2])
i = 0
for smp in self.samples:
smp_len = len(smp[0])
self.random_points[i:i+smp_len,0] = smp[0]
self.random_points[i:i+smp_len,1] = smp[1]
i += smp_len
# M条数据,每条数据N个特征
self.M, self.N = self.random_points.shape
# 加载数据
def loadData(self, filepath):
with open(filepath) as fr:
return pickle.load(fr)
def kmedoids(self, K):
# 初始化聚类点
centroids = self.initial(K)
dist = np.zeros([self.M, K])
cost = np.inf
threshold = 1e-3
while True:
cur_cost = 0.
# 计算每个点到当前各个聚类点的距离
for k in range(K):
dist[:,k] = np.sqrt(np.sum(np.power(self.random_points-centroids[k], 2), 1))
# 更新聚类点
for k in range(K):
all_ind = np.argmin(dist, 1)
dist_ind = (all_ind==k).nonzero()[0]
k_points = self.random_points[dist_ind,:]
dist_sum = np.zeros([len(k_points)])
# 这里和kmeans不同,计算每个点到其他点的距离
for i, point in enumerate(k_points):
dist_sum[i] = np.sum(np.sqrt(np.sum(np.power((self.random_points[dist_ind,:]-point), 2),1)))
# 选出距离和最小的点作为聚类点
best = dist_sum.argmin()
centroids[k] = k_points[best]
cur_cost += np.sum(dist_sum[best])
print cur_cost
# 如果收敛,则跳出循环
if abs(cur_cost-cost)<threshold:
break
cost = cur_cost
# self.centroids = centroids
# self.dist = dist
return dist, centroids
def initial(self, K, all=None):
if all is None:
return self.random_points[np.random.choice(range(0,self.M), K, replace=False)]
else:
return self.random_points[np.random.choice(all, K, replace=False)]
def draw(self, dist):
plt.figure(1)
all_ind = np.argmin(dist, 1)
color = ['r', 'g', 'b']
for k in range(self.K):
x, y = self.random_points[(all_ind==k).nonzero()[0],0],self.random_points[(all_ind==k).nonzero()[0],1]
plt.scatter(x, y , c=color[k])
plt.show()
if __name__ == '__main__':
km = Kmeans()
dist, _ = km.kmedoids(3)
km.draw(dist)
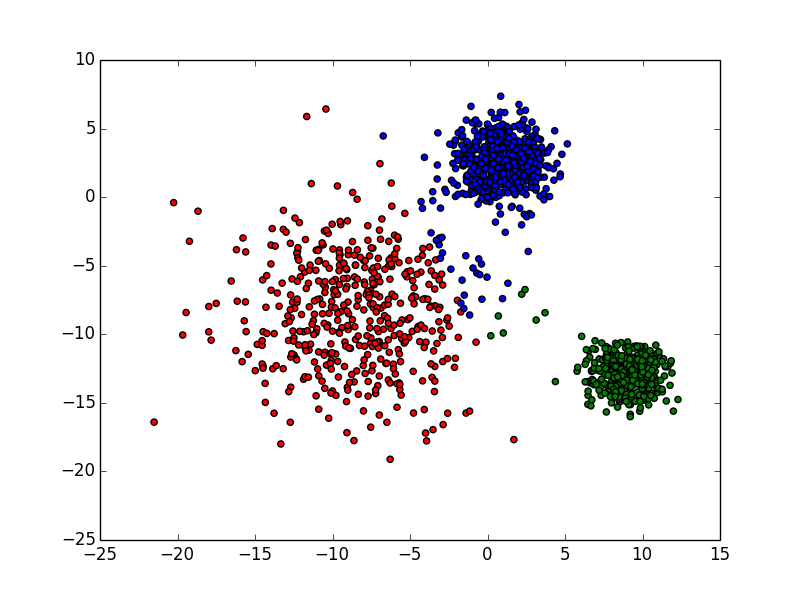
结果
原数据

聚类结果
3.Gaussian Mixture Model(GMM)
k-means是给每个数据点分配到具体的簇,而GMM的思路则是更贝叶斯。它不给出每个数据点对应的簇,而是给出每个数据点由各个聚类点产生的概率,并且不同聚类点产生某个数据点的概率和为1。
GMM的目的是,假定k个簇中每个簇产生的数据点满足n维高斯分布,估计产生目前观测的数据点的概率最大的k个簇的参数。即我们对下面的公式求最大值:
考虑到各个数据点的分布独立,则有:
\[p(x)=\prod_{i=1}^N p(x_i)=\displaystyle \sum_{i=1}^N \sum_{k=1}^K \pi_k \mathcal{N}(x_i|\mu_k, \Sigma_k)\]考虑单个数据点的概率比较小,许多很小的数字相乘起来在计算机里很容易造成浮点数下溢,因此我们使用对数处理上式:
\[\log p(x)=\displaystyle \sum_{i=1}^N \log \left\{\sum_{k=1}^K \pi_k \mathcal{N}(x_i|\mu_k, \Sigma_k)\right\}\]下面通过EM算法迭代求解参数$\mu_k$、$\pi_k$和$\Sigma_k$:
- E步
- 对于每个数据$x_i$来说,它由第k个聚类点生成的概率为: \(\displaystyle \gamma(i, k) = \frac{\pi_k \mathcal{N}(x_i|\mu_k, \Sigma_k)}{\sum_{j=1}^K \pi_j\mathcal{N}(x_i|\mu_j, \Sigma_j)}\)
- 在计算$\gamma(i, k)$的时候我们假定$\mu_k$和$\Sigma_k$均已知,我们将取上一次迭代所得的值(或者初始值)
- M步
- \[\displaystyle \begin{aligned} \mu_k & = \frac{1}{N_k}\sum_{i=1}^N\gamma(i, k)x_i \\ \Sigma_k & = \frac{1}{N_k}\sum_{i=1}^N\gamma(i, k)(x_i-\mu_k)(x_i-\mu_k)^T \\ \pi_k & = \frac{N_k}{N} \end{aligned}\]
- 其中$N_k = \sum_{i=1}^N \gamma(i, k)$,N为总数据点数。
重复迭代E、M两步,直到对数似然函数的值收敛为止。一般到M步停止收敛。
当$\Sigma$为奇异矩阵时,即它的行列式等于0,此时计算概率的时候会出现问题(概率会等于0),需要另外处理。比如可以在$\Sigma$的对角线上加一个较小值。具体可以看参考链接。
实现
# -*- encoding:utf-8 -*-
import numpy as np
from numpy import linalg
import sys
import time
import pickle
reload(sys)
sys.setdefaultencoding('utf8')
class GMM():
def __init__(self, k=3, filepath='../data/cluster.pkl'):
self.samples = self.loadData(filepath)
# K个聚类点component
self.K = k
# 数据预处理
self.random_points = np.zeros([len(self.samples)*len(self.samples[0][0]), 2])
i = 0
for smp in self.samples:
smp_len = len(smp[0])
self.random_points[i:i+smp_len,0] = smp[0]
self.random_points[i:i+smp_len,1] = smp[1]
i += smp_len
# M条数据,每条数据N个特征
self.M, self.N = self.random_points.shape
# 用k均值的思路初始化所有参数
def initial(self):
centroids = np.random.choice(range(self.M), self.K)
centroids = self.random_points[centroids]
# 1*K,即各个聚类的概率
ppi = np.zeros([self.K])
# K*N,即各个聚类点坐标
pmiu = centroids
# K*N*N,即各个聚类点的方差
psigma = np.zeros([self.K, self.N, self.N])
# M*K,距离矩阵
distmat = np.tile(np.sum(self.random_points**2, 1).reshape([-1,1]), (1, self.K)) + \
np.tile(np.sum(pmiu**2, 1).reshape([1,-1]), (self.M, 1)) - \
2*self.random_points.dot(np.transpose(pmiu))
# 初始化参数
distind = distmat.argmin(1)
for k in range(self.K):
# 得到每个类的索引
cur_ind = (distind==k).nonzero()[0]
# 得到每个类的数据比例
ppi[k] = float(len(cur_ind))/len(distind)
# 得到每个类的协方差矩阵,N*N
psigma[k,:,:] = np.cov(self.random_points[cur_ind].transpose())
return ppi, pmiu, psigma
def gmm(self):
ppi, pmiu, psigma = self.initial()
# 门限
threshold = 1e-10
Loss = -np.inf
iter = 1
while True:
# M*K
Pc = self.getProb(ppi, pmiu, psigma)
# M*K
gama = Pc*ppi
gama = gama / np.sum(gama, 1).reshape(-1,1)
# K*1
Nk = np.sum(gama, 0).flatten()
# 先计算协方差矩阵
for k in range(self.K):
shift = self.random_points-pmiu[k,:]
psigma[k,:,:] = (np.transpose(shift).dot(np.diag(gama[:,k]).dot(shift)))/Nk[k]
# 计算pi
ppi = Nk/self.M
# 计算miu
pmiu = (np.dot(np.transpose(gama), self.random_points))/Nk.reshape([-1,1])
# 也不一定是损失,只要使用一个会收敛的数值进行收敛判断就行,比如各个点到各自聚类点的距离之和
curLoss = -np.sum(np.log(Pc.dot(ppi.reshape(self.K, 1))))
# 判定是否收敛
if abs(curLoss-Loss)<threshold:
break
Loss = curLoss
print "Cur Loss:",Loss
iter += 1
self.Pc = Pc
self.miu = pmiu
self.gama = gama
self.pi = ppi
return Pc
def getProb(self, ppi, pmiu, psigma):
# N(x|pMiu,pSigma) = 1/((2pi)^(N/2))*(1/(abs(sigma))^0.5)*exp(-1/2*(x-pmiu)'psigma^(-1)*(x-pmiu))
Pc = np.zeros([self.M, self.K])
pi = np.pi
N = self.N
# 根据n维高斯公式计算概率密度矩阵
for k in range(self.K):
curp = psigma[k,:,:]
sigma_inverse = linalg.pinv(curp)
sigma_det = linalg.det(sigma_inverse)
if sigma_det < 0:
sigma_det = 0.
shift = self.random_points - pmiu[k,:]
Pc[:,k] = (1./((2*pi)**(N/2)))*(np.sqrt(np.abs(sigma_det)))*np.exp(-0.5*np.sum(np.dot(shift,sigma_inverse)*shift, 1)).flatten()
# M*K
return Pc
# 加载数据
def loadData(self, filepath):
with open(filepath) as fr:
return pickle.load(fr)
# 绘制图形
def draw(self, dataxy):
from matplotlib import pyplot as plt
plt.figure(1)
plt.scatter(dataxy[:,0],dataxy[:,1])
plt.show()
# 绘制聚类图形
def drawCluster(self):
from matplotlib import pyplot as plt
plt.figure(1)
all_ind = np.argmax(self.Pc, 1)
color = ['r', 'g', 'b']
for k in range(self.K):
print (all_ind==k).nonzero()[0]
x, y = self.random_points[(all_ind==k).nonzero()[0],0],self.random_points[(all_ind==k).nonzero()[0],1]
plt.scatter(x, y , c=color[k])
plt.show()
if __name__ == '__main__':
gmm = GMM()
gmm.gmm()
gmm.draw(gmm.random_points)
gmm.drawCluster()
结果
原数据

聚类结果